¡Qué mejor forma para empezar el año que dándole al bombo! El 29 de enero Eurovisión 2018 empezará a tomar forma con el reparto de los países en dos semifinales. En el primer blog de este año vamos a echar un vistazo a cómo se forman estas semifinales y a plantear un método alternativo que aplicaremos a los países de este año.
BAILANDO AL SON DEL BOMBO
Corría el año 2008, hace ya una década, cuando la organización del Festival se decidió a implantar dos semifinales debido al abultado número de países participantes. Después de la semifinal de récord en Helsinki 2007, donde participaron 28 países, se decidió separar a las naciones participantes en dos semifinales. Pero esta división no fue al tuntún.
Por entonces, el sistema de votación imperante era el televoto, que cada año mostraba los intercambios entre países afines. Por eso, para que no quedaran todos los amigos en la misma semifinal, la UER se inventó un sistema de bombos al más puro estilo de Copa Mundial de Fútbol, dividiendo a las naciones participantes según sus afinidades. De esta forma se garantizaba que el reparto de países entre ambas semifinales. Pero, como en todo, pagan justos por pecadores.
Analicemos lo que va a pasar este año. El 12 de enero se publicaron los bombos para las semifinales de Lisboa. Observando los integrantes vemos que hay grupos bien diferenciados, como el yugoslavo, el nórdico o el soviético. El cuarto se corresponde con países del sureste europeo, que no encajaban tanto en el yugoslavo o el soviético. El sexto es en realidad una mezcla de dos grupos, la triada báltica y Polonia junto a los dos países participantes del Benelux. Sin duda el más llamativo es el cinco, que es una amalgama con todo lo que sobraba: solo dos de sus países limitan entre sí.
| Bombo 1 | Bombo 2 | Bombo 3 | Bombo 4 | Bombo 5 | Bombo 6 |
| Albania | Dinamarca | Armenia | Bulgaria | Australia | Bélgica |
| Croacia | Finlandia | Azerbaiyán | Chipre | Austria | Estonia |
| FYR Macedonia | Islandia | Bielorrusia | Grecia | Chequia | Letonia |
| Montenegro | Irlanda | Georgia | Hungría | Israel | Lituania |
| Serbia | Noruega | Rusia | Moldavia | Malta | Países Bajos |
| Eslovenia | Suecia | Ucrania | Rumanía | San Marino | Polonia |
| Suiza | | | | | |
Ahora pasemos a la acción con un desafío visual. Calculando las votaciones medias del televoto de estos países a lo largo de la historia y ordenándolos según estos grupos, obtenemos la siguiente tabla (las columnas indican el voto a las filas). Y digo reto visual porque no se trata de estudiar las medias una a una sino de ver el mapa de calor de las votaciones. Si os fijáis, ahí donde se cruza cada grupo consigo mismo (es decir, cómo se votan entre sí los integrantes de cada grupo) podéis ver una alta concentración de puntos (zonas en rojo) en los cruces de los bombos 3 (soviético), 1 (yugoslavo) y 2 (nórdico). En el resto de grupos la concentración no es tan evidente, incluso, otros cruces, como los países del sureste votando a los soviéticos parecen tener mejores medias. Por tanto, a simple vista ya estamos viendo que estas agrupaciones sí tienen sentido para ciertos países, pero no para otros.
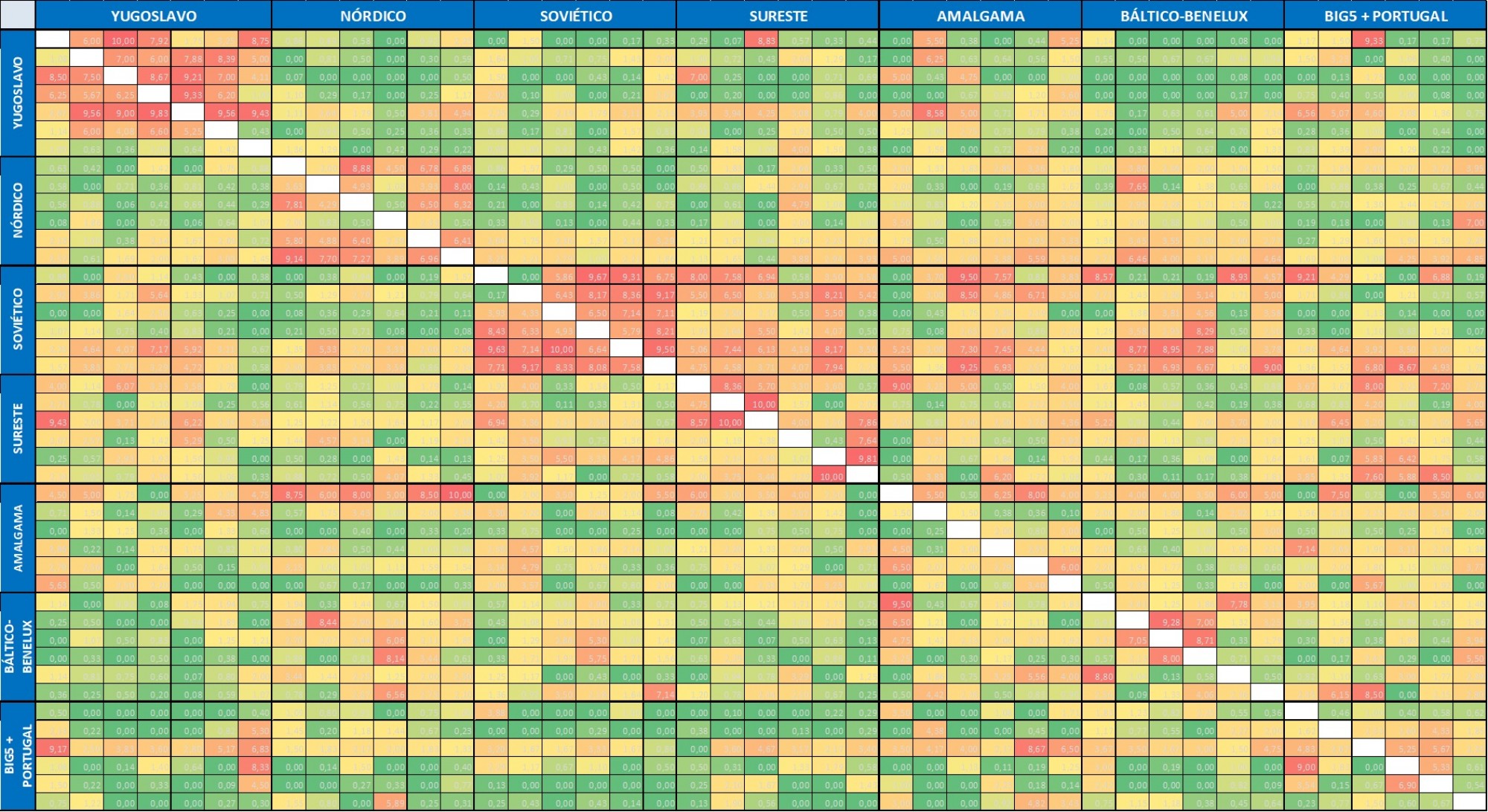
Saquemos ahora los números a la luz y extraigamos la media de las medias en cada cruce. El resultado lo podéis ver en la siguiente tabla. Como veíamos antes, los cruces de los bombos 1, 2 y 3 son los mejores cruces para cada bombo. No ocurre lo mismo con los bombos 4, 5 y 6. En estos tres bombos, la mejor media la otorgan al bombo 3 de países soviéticos. A pesar de esto, la segunda mejor media de cada grupo si es la del cruce consigo mismo. Incluso el grupo de países con acceso directo a la final otorga unas medias a cada grupo bastante homogéneas.
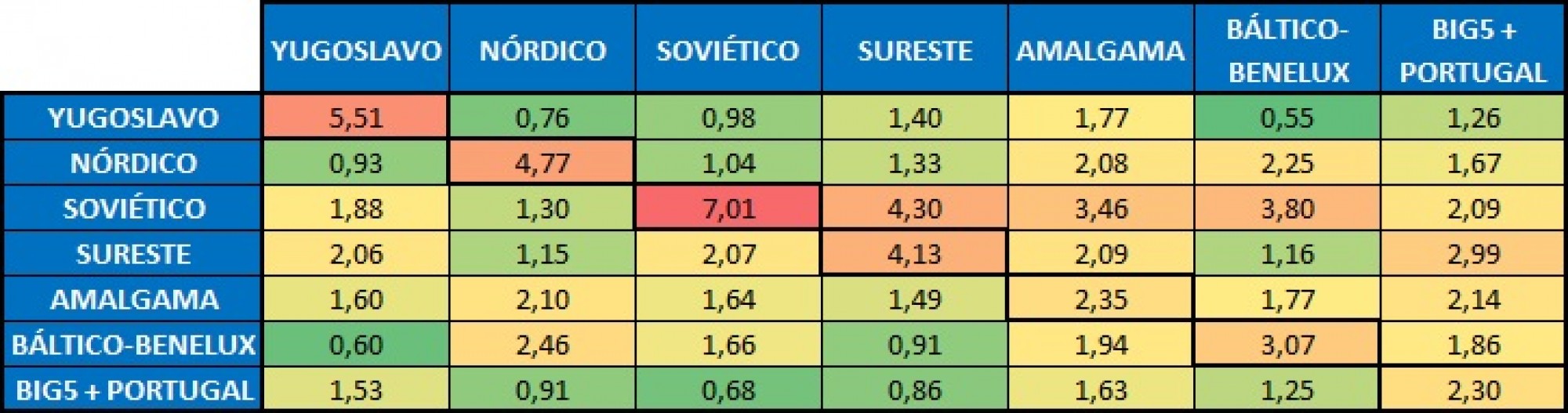
Lo bueno de este sistema de bombos es que es simple, se entiende fácil y evita que grandes grupos de países queden alojados en la misma semifinal.
Sin embargo, esta tampoco tendría que ser la única solución. Las inclinaciones de voto que acabamos de ver sugieren que los tres países soviéticos en cada semifinal, ya cuentan seguro con dos 7 de media, mientras que tres países del bombo 5 apenas se garantizan dos medias de 2,3.
Como digo, este es una forma simple y efectiva de solventar el problema. Pero, ¿se puede alcanzar alguna solución más óptima aunque sea más compleja?
BUSCANDO EL ÓPTIMO MATEMÁTICO
Tengamos en cuenta que lo que queremos es evitar que países muy afines entre sí queden en la misma semifinal. Para ello vamos a suponer este pequeño ejemplo donde tenemos cuatro países que votan de la siguiente forma y que queremos dividir en dos semifinales de dos países.
| A | B | C | D |
| A | – | 8 | 6 | 0 |
| B | 10 | – | 3 | 3 |
| C | 7 | 8 | – | 6 |
| D | 3 | 5 | 4 | – |
Para analizar la afinidad entre países, tomemos en cuenta los promedios de sus votos. Por ejemplo, A otorga a B 10 puntos de media y B otorga a A 8 puntos de media. El promedio de 10 y 8 es 9. Como es el mismo de A a B que de B para A, lo representamos solo una vez, quedando esta tabla triangular.
El mayor de estos intercambios se da entre los países A y B, por tanto, nos interesará que cada uno esté en una semifinal distinta. Ahora que ya sabemos que no queremos que A y B se junten, buscamos el siguiente máximo. Este se da ahora entre A y C por tanto, no querremos que A y C se junten. En definitiva, A solo debería estar con D y por descarte B estará en la misma semifinal que C. Es decir, con el método del promedio las semifinales serían A-D y B-C.
Esta forma de repartir a los países se ha hecho en base a los intercambios promedio, pero sabemos por experiencia que los países no siempre son afines entre sí, sino que a veces es uno el que vota alto por el otro pero no al revés. Por eso vamos a plantear un método de máximos, es decir, en vez de hacer el promedio nos quedaremos con la cifra más alta de los intercambios. Por ejemplo, analizando el caso de A y B, el máximo entre 10 y 8 es 10. Como es lo mismo de A a B que de B a A lo introducimos una sola vez mostrando una tabla triangular como la que sigue.
Siguiendo los mismos pasos, la mayor vinculación sigue siendo A con B, por tanto no los juntaremos en la misma semifinal. Después está la relación entre B y C, que tampoco deberían juntarse. Esto nos lleva a que B solo puede juntarse con D. Por tanto, con el método de máximos las semifinales serían A-C y B-D. Como veis para este caso ambos criterios dan un resultado diferente.
Y SI…
Pasemos ahora de la teoría a la práctica. Tomemos la tabla de votaciones medias por televoto de los países semifinalistas (sin tener en cuenta los bombos) y apliquemos el método del máximo. ¿Cuáles serían las semifinales utilizando este método?
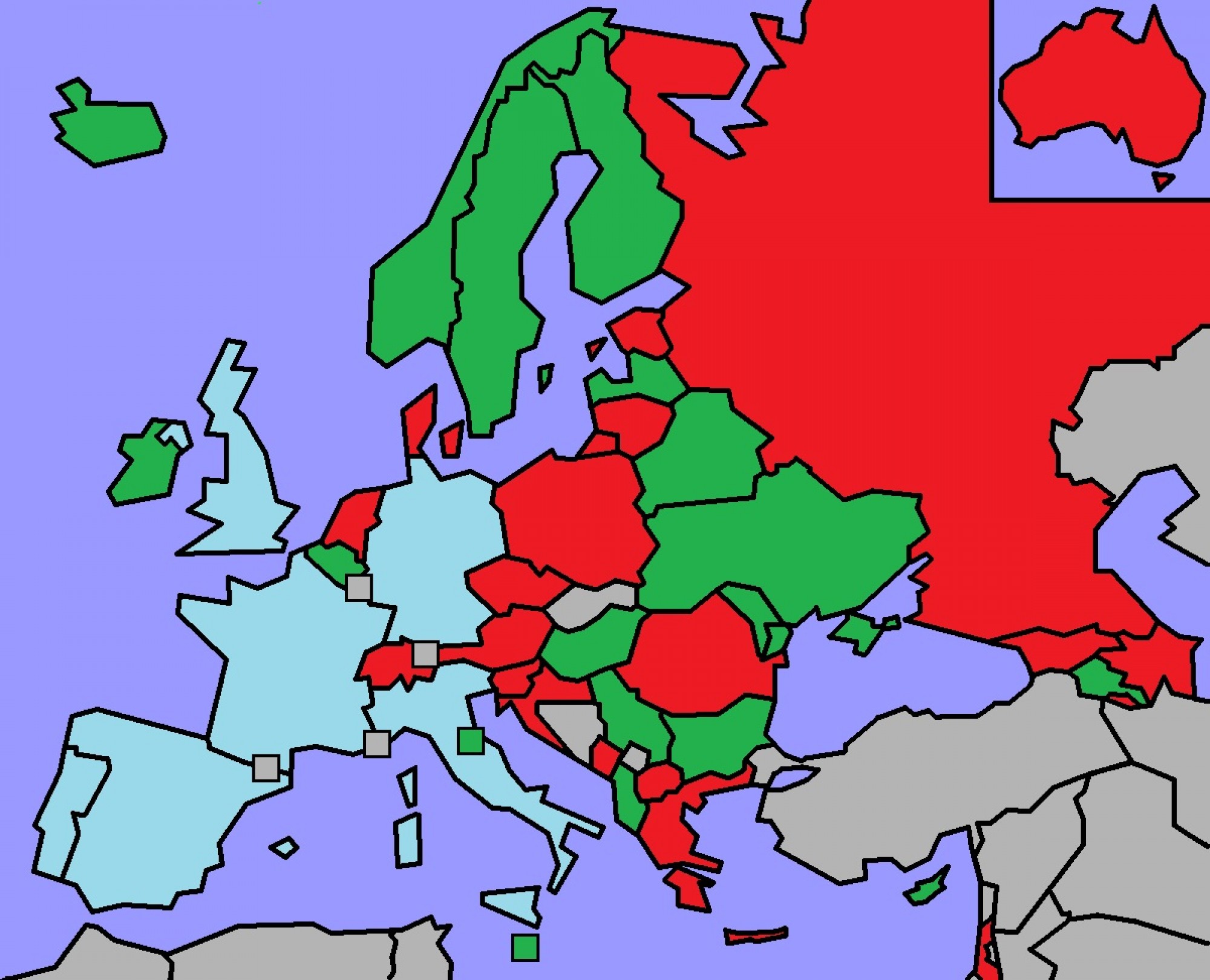
A continuación podéis ver la tabla con las dos semifinales que se alcanzan con este método y su representación gráfica en el mapa.
SEMIFINAL 1
(rojo) | SEMIFINAL 2
(verde) |
| Australia | Albania |
| Austria | Armenia |
| Azerbaiyán | Bélgica |
| Chequia | Bielorrusia |
| Croacia | Bulgaria |
| Dinamarca | Chipre |
| Eslovenia | Finlandia |
| Estonia | Hungría |
| FYR Macedonia | Irlanda |
| Georgia | Islandia |
| Grecia | Letonia |
| Israel | Malta |
| Lituania | Moldavia |
| Montenegro | Noruega |
| Países Bajos | San Marino |
| Polonia | Serbia |
| Rumanía | Suecia |
| Rusia | Ucrania |
| Suiza | |
Con respecto al primer bombo, el de países yugoslavos, vemos lo descompensado que está: Serbia y Albania se separan de los otros cinco. Esto es así por la gran ventaja que toman los dos del resto, especialmente Serbia. Gráficamente podéis ver en el mapa como al incluir a Serbia en una semifinal distinta, el resto de yugoslavos quedan separados.
Lo mismo ocurre con los nórdicos, donde sólo Dinamarca se separa del resto de su bombo. En realidad, el bombo en vez de incluir a Irlanda deberían haber metido a Australia, que está precisamente en la misma semifinal que Dinamarca. De esta forma estos dos países se separan de Finlandia, Islandia, Noruega y Suecia.
El grupo soviético si se reparte equitativamente, tres en cada lado. En cuanto al de países del sureste tenemos un reparto desigual 2 a 4. En verdad este bombo lo tendríamos que dividir en dos triadas: Grecia, Chipre y Bulgaria por un lado; y Rumanía, Hungría y Moldavia por otro. Grecia y Rumanía son los más beneficiados en cada triada y por eso este método los separa de sus afines.
El sexto bombo como era de esperar separa a Bélgica de Países Bajos. Y en cuanto a los tres países bálticos, el central, Letonia, es el que se va a la semifinal contraria. Polonia, que estaba un poco más descolgado en este bombo, recae ahí para no estar con Ucrania.
Por último, el quinto bombo, con el resto de países, se reparte también de forma desigual. Aunque esto no sería así si la organización hubiese intercambiado los grupos de Australia e Irlanda tal y como mencionaba anteriormente.
En definitiva, esta es una combinación que no llegaremos a ver en Lisboa, pero que después de todo, no dista mucho de la que pudiera crearse con el sistema de bombos. Ahora solo nos queda esperar a ver qué sucede y confiar en que las semifinales no estén descompensadas. Porque, aunque dependerá mucho del nivel musical, una ayudita vecinal siempre puede decidir el último clasificado.
Aquí finalizo mi reflexión sobre los bombos. ¿Te parece justo el reparto de los bombos? ¿Crees que las semifinales que propongo son razonables? ¿Se te ocurre otra forma de repartir a los países? Lo dicho, el 29 de enero todos pendientes de cómo quedan repartidas. ¡Suerte a todos!