La portavoz de Dinamarca, Ulla Essendrop, dando los votos daneses en 2016
La UER sigue en busca del sistema de votación perfecto. Este año cumplimos 10 años desde el regreso de los jurados al concurso y el historial de cambios en el sistema de votaciones no ha hecho más que incrementarse desde entonces. Para este año, las clasficaciones de los jurados se interpretarán de otra forma: de lineal a exponencial. En la noticia ya hemos explicado cómo funciona. Pero como con casi todo en esta vida, con un ejemplo todo se ve mucho mejor… y si son dos, pues mejor aún.
DE LINEAL A EXPONENCIAL
Antes de entrar en materia vamos a ver cómo funciona. Los 5 jurados de cada nación van a seguir haciendo sus propias clasificaciones de países, ordenándolos del 1 al 26 o 27 en función de sus preferencias. Hasta ahí todo es como hasta ahora. El cambio viene en que las posiciones van a tener un valor diferente. Este valor hasta ahora era lineal porque la diferencia entre cualquier puesto es la misma: del primero al segundo hay 1 de distancia, del decimoquinto al decimosexto también hay 1 de distancia, y así entre cualquier posición consecutiva.
Con el cambio, estas diferencias ya no son las mismas en función de donde nos encontremos: la diferencia entre el primero y el segundo puede ser de 1 pero la diferencia entre el decimoquinto y el decimosexto puede ser 0,6. En el ejemplo de Eurovisión estamos ante una exponencial decreciente: las diferencias entre los puestos van siendo cada vez menores, de tal forma que hay una gran diferencia entre ser primero y segundo, pero apenas la habrá entre ser penúltimo y último, a pesar de que en ambos casos solo hay un puesto de diferencia.
EL MINI-EJEMPLO
Fijaos en este sencillo método de votación. La primera columna tiene el método lineal, porque la diferencia entre puestos consecutivos siempre es la misma, en este caso, 6. La segunda columna representa una votación exponencial. En este caso, las diferencias entre los puestos van decayendo: 9, 7, 5 y 3.
| Orden | Lineal | Exponencial |
| 1º | 25 | 25 |
| 2º | 19 | 16 |
| 3º | 13 | 9 |
| 4º | 7 | 4 |
| 5º | 1 | 1 |
Supongamos un jurado compuesto por dos personas que opinan justo al contrario. Con el método lineal, todos los países obtendrían 26 puntos (ver tabla). En cambio, con el método exponencial, aquellos que obtuvieron un primer puesto quedan por delante en la clasificación. Les siguen los que tuvieron un segundo y el último sería el que consiguió los dos terceros puestos, las posiciones intermedias. Por tanto, ya vemos que una primera posición ahora resulta más beneficiosa que con el método lineal.
| LINEAL | JURADO «A» | JURADO «B» | TOTAL | CLASIFICACIÓN |
| País A | 25 | 1 | 26 | 1º |
| País B | 19 | 7 | 26 | 1º |
| País C | 13 | 13 | 26 | 1º |
| País D | 7 | 19 | 26 | 1º |
| País E | 1 | 25 | 26 | 1º |
| EXPONENCIAL | JURADO «A» | JURADO «B» | TOTAL | CLASIFICACIÓN |
| País A | 25 | 1 | 26 | 1º |
| País B | 16 | 4 | 20 | 3º |
| País C | 9 | 9 | 18 | 5º |
| País D | 4 | 16 | 20 | 3º |
| País E | 1 | 25 | 26 | 1º |
Ahora vamos a considerar el mismo caso pero tenemos dos jurados que piensan igual y uno que piensa al revés. En el ejemplo del método lineal, el jurado «C», el díscolo, no tiene ninguna influencia sobre la clasificación final y los otros dos jurados consiguen imponer su criterio. Con el exponencial, en cambio, el jurado «C» consigue impulsar al país E hasta el tercer puesto, por el beneficio que le supone tener una primera posición.
| LINEAL | JURADO «A» | JURADO «B» | JURADO «C» | TOTAL | CLASIFICACIÓN |
| País A | 25 | 25 | 1 | 51 | 1º |
| País B | 19 | 19 | 7 | 45 | 2º |
| País C | 13 | 13 | 13 | 39 | 3º |
| País D | 7 | 7 | 19 | 33 | 4º |
| País E | 1 | 1 | 25 | 27 | 5º |
| EXPONENCIAL | JURADO «A» | JURADO «B» | JURADO «C» | TOTAL | CLASIFICACIÓN |
| País A | 25 | 25 | 1 | 51 | 1º |
| País B | 16 | 16 | 4 | 36 | 2º |
| País C | 9 | 9 | 9 | 27 | 3º |
| País D | 4 | 4 | 16 | 24 | 5º |
| País E | 1 | 1 | 25 | 27 | 3º |
Es decir, las dos grandes consecuencias de este cambio son: uno, «es mejor tener una buena posición y una mala que dos mediocres»; y dos, los jurados díscolos tendrán más capacidad para impulsar a sus países favoritos.
UN EJEMPLO REAL: HILDA HEIK, LA JURADO «DÍSCOLA»Si has entendido el ejemplo anterior y quieres saber más, es momento de estudiar un caso real. Probablemente su nombre no te sea familiar, pero en 2016 esta jurado de Dinamarca fue noticia por haberse equivocado a la hora de votar en la final de Estocolmo. A diferencia de sus compañeros, Hilda se confundió al elaborar su clasificación y la hizo al revés. En la siguiente tabla puedes ver cómo votó el jurado de Dinamarca en 2016 y descubrirás rápidamente que Hilda era la jurado D:
| PAÍS | JURADO
A | JURADO
B | JURADO
C | JURADO
D | JURADO
E | RANKING
JURADO |
 | UCRANIA | 3 | 14 | 4 | 2 | 5 | 1 |
 | AUSTRALIA | 1 | 1 | 1 | 26 | 1 | 2 |
 | BÉLGICA | 8 | 8 | 3 | 22 | 3 | 3 |
 | PAÍSES BAJOS | 12 | 6 | 2 | 25 | 4 | 4 |
 | BULGARIA | 4 | 17 | 7 | 16 | 6 | 5 |
 | LITUANIA | 7 | 7 | 13 | 15 | 11 | 6 |
 | SUECIA | 17 | 10 | 5 | 20 | 2 | 7 |
 | REINO UNIDO | 5 | 25 | 8 | 11 | 7 | 8 |
 | ISRAEL | 2 | 16 | 11 | 19 | 9 | 9 |
 | ESPAÑA | 6 | 3 | 22 | 21 | 8 | 10 |
 | ARMENIA | 20 | 5 | 15 | 4 | 21 | 11 |
 | ITALIA | 13 | 11 | 14 | 18 | 12 | 12 |
 | RUSIA | 11 | 9 | 9 | 24 | 15 | 13 |
 | FRANCIA | 18 | 2 | 6 | 23 | 20 | 14 |
 | LETONIA | 19 | 4 | 18 | 13 | 16 | 15 |
 | CHIPRE | 9 | 21 | 26 | 9 | 10 | 16 |
 | AUSTRIA | 26 | 15 | 10 | 7 | 18 | 17 |
 | SERBIA | 22 | 12 | 25 | 5 | 14 | 18 |
 | CHEQUIA | 16 | 19 | 17 | 10 | 19 | 19 |
 | MALTA | 24 | 13 | 19 | 8 | 17 | 20 |
 | GEORGIA | 10 | 23 | 24 | 1 | 24 | 21 |
 | CROACIA | 23 | 22 | 12 | 3 | 25 | 22 |
 | ALEMANIA | 14 | 24 | 20 | 6 | 23 | 23 |
 | HUNGRÍA | 21 | 20 | 16 | 12 | 22 | 24 |
 | POLONIA | 15 | 18 | 21 | 17 | 26 | 25 |
 | AZERBAIYÁN | 25 | 26 | 23 | 14 | 13 | 26 |
En las siguientes tablas puedes ver cómo votó el jurado danés, cómo habrían votado en caso de que Hilda no se hubiese equivocado y cómo habrían votado si se hubiese prescindido de los votos de Hilda. El cambio más notable si se hubiesen corregido los votos de Hilda habría sido que Ucrania pasaría de 12 puntos a no recibir ninguno. Por eso este caso es un gran ejemplo de qué pasaría con el nuevo sistema de jurados que se implanta en 2018: ¿cuál es el efecto si un jurado piensa muy diferente a los demás?
LO QUE VOTARON
LOS JURADOS | LO QUE DEBIÓ HABER
VOTADO EL JURADO | LO QUE HABRÍAN
VOTADO SIN HILDA |
 | UCRANIA | 12 |  | AUSTRALIA | 12 |  | AUSTRALIA | 12 |
 | AUSTRALIA | 10 |  | PAÍSES BAJOS | 10 |  | BÉLGICA | 10 |
 | BÉLGICA | 8 |  | BÉLGICA | 8 |  | PAÍSES BAJOS | 8 |
 | PAÍSES BAJOS | 7 |  | SUECIA | 7 |  | UCRANIA | 7 |
 | BULGARIA | 6 |  | BULGARIA | 6 |  | BULGARIA | 6 |
 | LITUANIA | 5 |  | ESPAÑA | 5 |  | SUECIA | 5 |
 | SUECIA | 4 |  | ISRAEL | 4 |  | ISRAEL | 4 |
 | REINO UNIDO | 3 |  | RUSIA | 3 |  | LITUANIA | 3 |
 | ISRAEL | 2 |  | FRANCIA | 2 |  | ESPAÑA | 2 |
 | ESPAÑA | 1 |  | LITUANIA | 1 |  | RUSIA | 1 |
LA CLAVE DE LOS PESOS
Como veíamos anteriormente, ahora ya no se trata de hacer una media de posiciones para saber la clasificación final del jurado. Con el método exponencial a cada posición se le asigna un peso que va decayendo según bajamos en la clasificación. Hay infinitas posibilidades para asignar estos pesos y es un misterio cuál usarán finalmente. Aún sin conocerlo podemos hacer varias simulaciones y ver cómo habrían afectado a los resultados del jurado de Dinamarca.
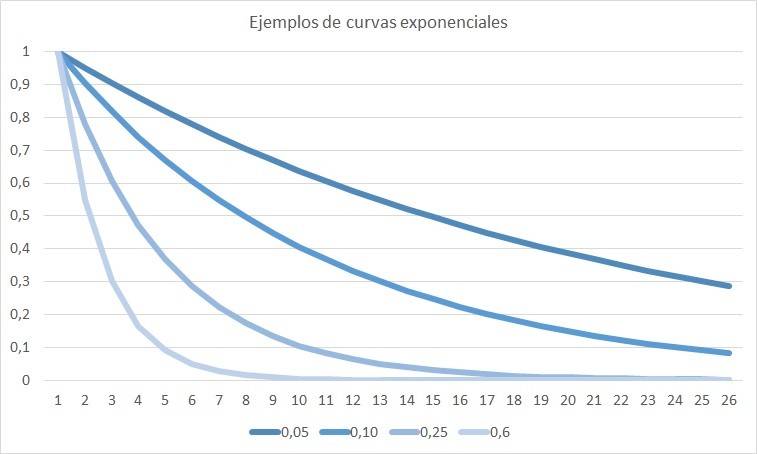
Estas simulaciones dependerán de la pendiente de la exponencial: si decae rápido o si lo hace lentamente. En el gráfico podéis ver exponenciales para diferentes pendientes y en las tablas cómo habrían quedado las votaciones de haber usado estas exponenciales decrecientes.
| 0,05 | 0,10 | 0,25 | 0,6 |
 | AUSTRALIA | 12 |  | AUSTRALIA | 12 |  | AUSTRALIA | 12 |  | AUSTRALIA | 12 |
 | UCRANIA | 10 |  | UCRANIA | 10 |  | UCRANIA | 10 |  | UCRANIA | 10 |
 | BÉLGICA | 8 |  | BÉLGICA | 8 |  | PAÍSES BAJOS | 8 |  | GEORGIA | 8 |
 | PAÍSES BAJOS | 7 |  | PAÍSES BAJOS | 7 |  | BÉLGICA | 7 |  | PAÍSES BAJOS | 7 |
 | BULGARIA | 6 |  | SUECIA | 6 |  | SUECIA | 6 |  | SUECIA | 6 |
 | SUECIA | 5 |  | BULGARIA | 5 |  | GEORGIA | 5 |  | BÉLGICA | 5 |
 | REINO UNIDO | 4 |  | ESPAÑA | 4 |  | FRANCIA | 4 |  | FRANCIA | 4 |
 | LITUANIA | 3 |  | REINO UNIDO | 3 |  | ESPAÑA | 3 |  | ISRAEL | 3 |
 | ISRAEL | 2 |  | ISRAEL | 2 |  | ISRAEL | 2 |  | ESPAÑA | 2 |
 | ESPAÑA | 1 |  | LITUANIA | 1 |  | BULGARIA | 1 |  | CROACIA | 1 |
Cuanto menor es el valor de la pendiente, más parecida es la votación a la que realmente fue. Vemos que Australia habría adelantado a Ucrania, aunque esta última no habría perdido más puestos. El más perjudicado es Lituania, que descendiende varios puestos. Si nos fijamos el país báltico obtiene posiciones medias de los jurados, meintras que sus rivales tienen alguna destacada y este método los impulsa para superar a Lituania. Es decir, destacar es más valioso que estar en la media, tal y como veíamos antes.
Cuando la pendiente aumenta, vemos el ascenso de Georgia, el falso top1 de Hilda, y Croacia, top3. Es decir, si la pendiente es demasiado elevada, este método exponencial puede conseguir justo el efecto contrario al deseado: premiar a aquellos países que solo han gustado a un jurado díscolo. Incluso para este caso, que es el que más perjudicaría a Australia, al tener al resto de jurados de su parte, consigue anular el 26º puesto que le daba Hilda y permanece en la cabeza.
En resumen, lo que vemos es que este método premiará a aquellos países que logren buenas posiciones con respecto a aquellos que obtengan posiciones medias o bajas. También, para valores bajos de pendiente, promoverá el consenso frente a opiniones independientes. Al favorecer el consenso se impulsará a los países favoritos en detrimento de los que menos gusten. Por tanto habrá más distancias entre unos y otros y con ello los jurados pueden discriminar (positivamente) más. Al final, este método exponencial resultará en un mayor peso del jurado con respecto al televoto.